Quantum computers the key to elusive ‘Theory of Everything’

Fig. 2. Light from distant stars is curved by the gravity of the sun before it reaches Earth.

During the first two decades of the 20th century, European science experienced a revolution. Albert Einstein’s Theory of Relativity offered a new model of the macrocosmos, while Niels Bohr and others developed the atomic model of the microcosmos.

However, the two models resisted integration into a “theory of everything.” At the heart of the problem appear to be two distinct forms of mathematics: discrete and continuous. But quantum computing may come to the rescue.

Discrete and continuous

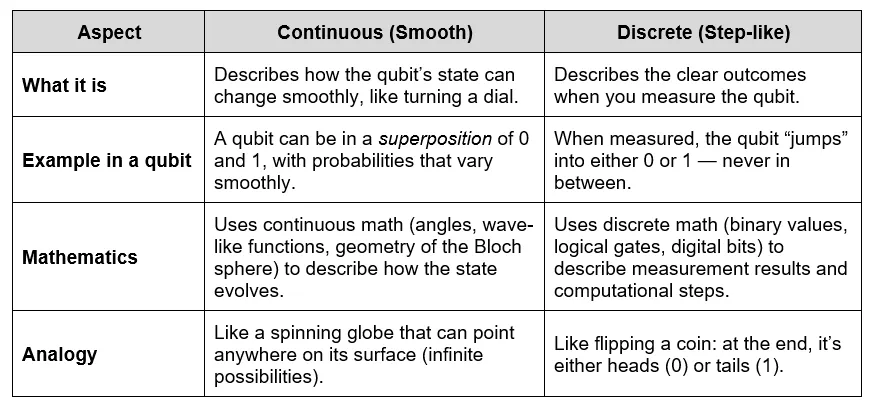
The distinction between discrete and continuous mathematics lies at the heart of modern physics and computer science. Discrete mathematics describes reality in separate, countable units—like the binary digits used in computing—while continuous mathematics captures smooth, unbroken processes, such as waves and curves.

This tension between the discrete and the continuous has shaped some of the most important breakthroughs in science, including quantum mechanics to relativity, and continues to influence new frontiers such as quantum computing.

At the turn of the 20th century, scientists believed light and radiation were continuous phenomena.

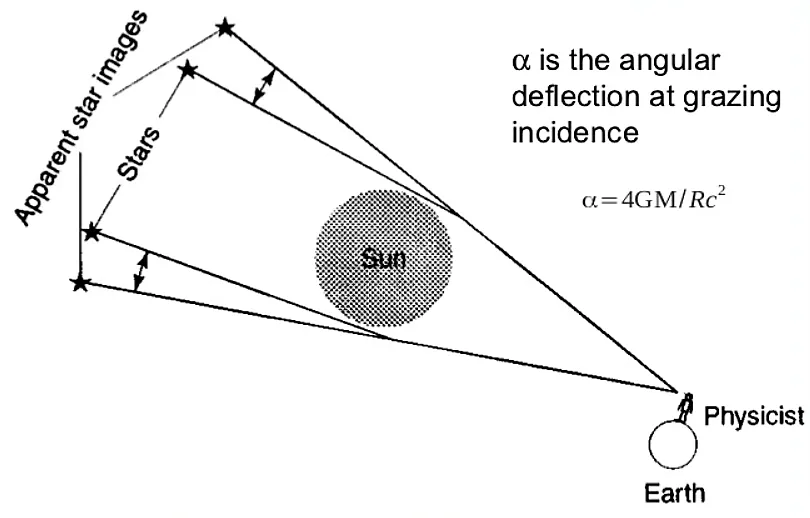
In 1900, German physicist Max Planck challenged this view. To formulate his radiation law, he treated light as discrete units, or quanta, a move dictated by mathematical necessity rather than experimental evidence. Planck initially regarded quanta as abstract mathematical constructs, not physical reality.

This step marked the entry of discrete mathematics into physics. Planck’s quantization is comparable to modern digital sampling: just as music is digitized by recording many tiny samples per second, Planck treated radiation as composed of discrete packets.

From quanta to photons

In 1905, Einstein gave new meaning to Planck’s idea of quanta by explaining the photoelectric effect. He proposed that light consists of discrete packets of energy, later called photons.

Experiments confirmed that light, long regarded as a continuous wave, could also behave like particles under certain conditions. Planck’s mathematical abstraction thus became Einstein’s physical reality, marking discreteness as a fundamental feature of nature.

Einstein’s work on the photoelectric effect paved the way for a new atomic model. Building on the idea that energy comes in discrete packets, Bohr proposed in 1913 that electrons orbit the nucleus in fixed energy levels and can jump between them by absorbing or emitting photons.

This explained atomic spectra, where light appears in distinct lines rather than continuous bands. Bohr’s model marked the beginning of quantum mechanics and laid the foundation for what would later become the Standard Model of particle physics, which unifies our understanding of fundamental particles and their interactions.

Notably, in that same year that Einstein published his paper on the photoelectric effect, in 1905, he also published his Special Theory of Relativity, in which he described space and time not as discrete but as continuous. In relativity, space and time are “classical”, i.e., Newtonian.

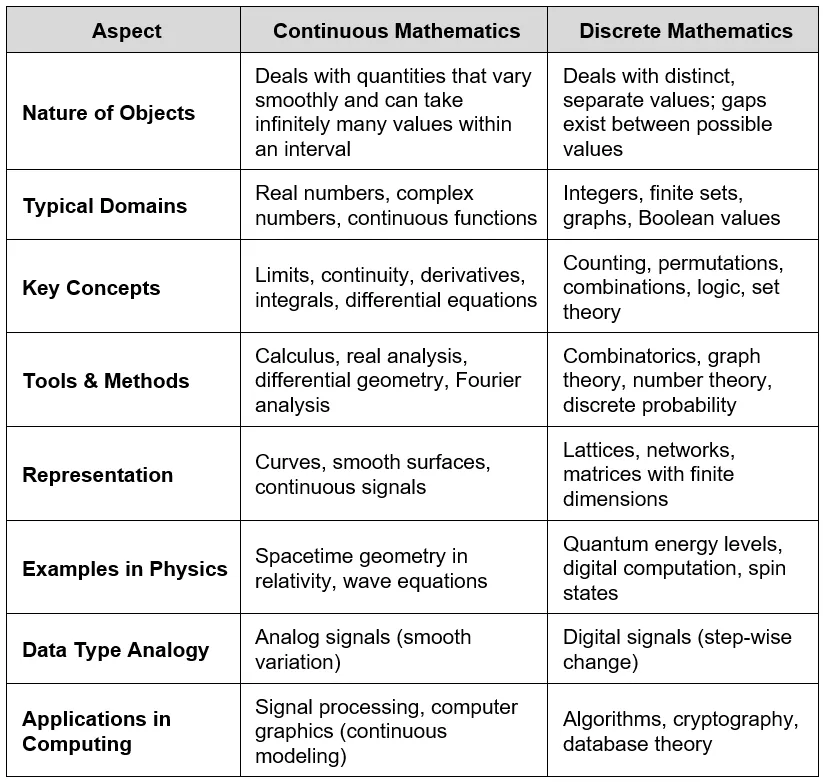
A decade later, Einstein’s General Relativity extended this continuous framework to gravity, describing it as the smooth, continuous curvature of spacetime. Confirmed by the 1919 eclipse expedition of physicist and astronomer Arthur Stanley Eddington, relativity became the foundation for understanding the macrocosmos.

In this way, Einstein advanced both sides of the great divide: the quantum world of discrete quanta and the relativistic universe of continuous spacetime. Yet these two pillars of physics remain mathematically incompatible, underscoring the unresolved challenge of uniting the discrete and the continuous in a single theory.

Hybrid models

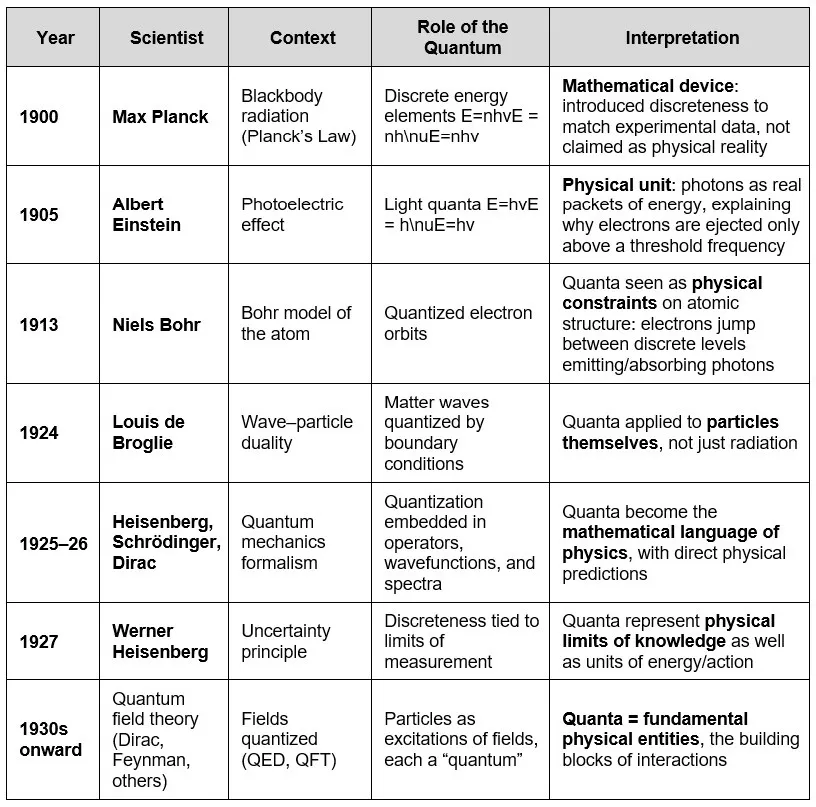
Efforts to reconcile relativity with quantum mechanics gave rise to hybrid models that weave together discrete and continuous mathematics. The three best-known examples are:

• Loop Quantum Gravity (LQG): Describes space as built from discrete “chunks” (spin networks), while its evolution unfolds through continuous geometry.
• String Theory: Envisions strings as continuous, vibrating objects whose modes of vibration produce discrete particle spectra.
• Quantum Field Theory (QFT): Treats fields as continuous entities, but their excitations manifest as discrete particles.

Each of these approaches represents an attempt to bridge the gap between discreteness and continuity, in effect seeking a unified framework for the fundamental structure of nature.

Quantum computing

Quantum computing, first proposed by American physicist Richard Feynman in the 1960s, brings the discrete-continuous puzzle into sharp relief.

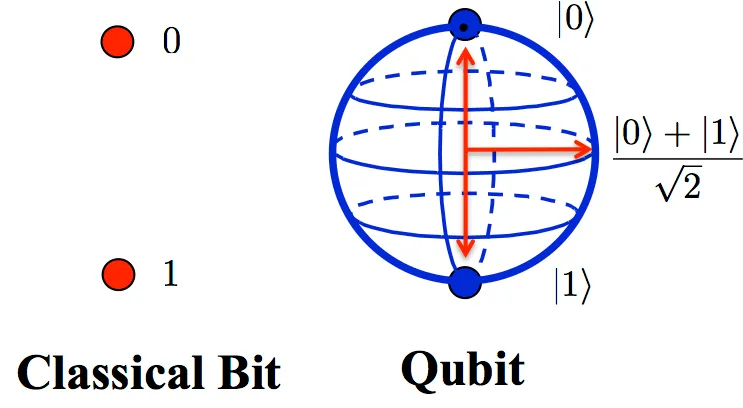
This third generation of computing, after analog and digital, computes with subatomic particles rather than with electronic currents. The computational unit of quantum computing, the qubit, embodies both discrete and continuous processes.

Like a classical bit, a qubit has two poles – 0 and 1 – but poles can exist in superposition, meaning it can be partly 0 and partly 1 at the same time, depending on the context and the state or surrounding qubits.

On the Bloch sphere, continuous operations are represented as points on its smooth surface. Computation uses the discrete (binary) states (0 and 1) for logic, while continuous (analog) rotations across the sphere govern the operations.

The real breakthrough comes when qubits are linked through entanglement, a phenomenon in which two or more qubits share the same quantum state no matter how far apart they are. This enables quantum computers to process multiple possibilities simultaneously, rather than one step at a time, as classical machines do.

This dual character – superposition and entanglement – gives quantum computers extraordinary power. Tasks such as simulating molecules with dozens of atoms, impossible for today’s fastest supercomputers, could be completed in minutes on a quantum machine.

Quantum computing may help resolve the dichotomies between quantum mechanics and Relativity, between wave and particle duality, and between continuous and discrete, thereby broadening our understanding of the universe.

Infinity in reach

For centuries, scientific progress has been driven by extending human senses through the use of instruments. Telescopes opened the heavens to reveal Earth’s place in the cosmos; particle colliders probe the tiniest scales, uncovering the particles of the Standard Model.

Now, the quantum computer may emerge as a new kind of instrument, not one that looks outward or smashes particles, but one that explores reality by simulation. It will allow physicists to model quantum fields, black holes and exotic states of matter in ways classical machines cannot. It may even be able to simulate the Big Bang.

Where telescopes opened the infinitely large and colliders the infinitely small, quantum computing may expand our grasp of the infinitely complex, and perhaps of infinity itself. It may even lead to the elusive Theory of Everything.

Jan Krikke is a journalist based in Thailand. His latest book is an AI-mediated bio titled “East and West at the Crossroads: Integrating Science, Ethics, and Consciousness Across Cultures.” It may be purchased here.